Snowflurry
Snowflurry est une bibliothèque d'informatique quantique à code source ouvert développée en Julia par Anyon Systèmes qui permet de construire, de simuler et d'exécuter des circuits quantiques. Une bibliothèque connexe nommée SnowflurryPlots permet de visualiser les résultats de la simulation dans un diagramme à bandes. Pratique pour explorer l'informatique quantique, les fonctionnalités sont disponibles dans la documentation et le guide d'installation est disponible sur la page GitHub. Tout comme la bibliothèque PennyLane, Snowflurry peut être utilisée pour exécuter des circuits quantiques sur l'ordinateur quantique MonarQ.
Installation
Le simulateur d'ordinateur quantique avec Snowflurry est disponible sur toutes nos grappes. Le langage de programmation Julia doit être chargé avant d'avoir accès à Snowflurry avec la commande
[name@server ~]$ module load julia
Ensuite, l'interface de programmation Julia est appelée et la bibliothèque quantique de Snowflurry chargée (environ 5-10 minutes) avec les commandes
[name@server ~]$ julia
julia> import Pkg
julia> Pkg.add(url="https://github.com/SnowflurrySDK/Snowflurry.jl", rev="main")
julia> Pkg.add(url="https://github.com/SnowflurrySDK/SnowflurryPlots.jl", rev="main")
julia> using Snowflurry
Les portes logiques quantiques et les commandes sont décrites dans la documentation de Snowflurry.
Exemple d'utilisation : États de Bell
Les états de Bell sont des états à deux qubits maximalement intriqués. Deux exemples simples de phénomènes quantiques sont la superposition et l'intrication. La bibliothèque Snowflurry permet de construire le premier état de Bell comme suit.
[name@server ~]$ julia
julia> using Snowflurry
julia> circuit=QuantumCircuit(qubit_count=2);
julia> push!(circuit,hadamard(1));
julia> push!(circuit,control_x(1,2));
julia> print(circuit)
Quantum Circuit Object:
qubit_count: 2
q[1]:──H────*──
¦
q[2]:───────X──
Dans la section de code ci-dessus, la porte de Hadamard crée une superposition égale de |0⟩ et |1⟩ sur le premier qubit tandis que la porte CNOT (porte X contrôllée) crée une intrication entre les deux qubits. On retrouve une superposition égale des états |00⟩ et |11⟩, soit le premier état de Bell. La fonction simulate permet de simuler l'état exact du système.
julia> state = simulate(circuit)
julia> print(state)
4-element Ket{ComplexF64}:
0.7071067811865475 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.7071067811865475 + 0.0im
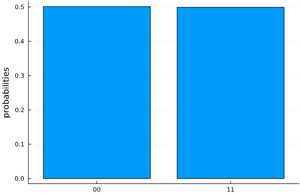
Pour prendre une mesure, l'opération readout permet de spécifier quels qubits seront mesurés. La fonction plot_histogram de la bibliothèque SnowflurryPlots permet de visualiser les résultats.
[name@server ~]$ julia
julia> using SnowflurryPlots
julia> push!(circuit, readout(1,1), readout(2,2))
julia> plot_histogram(circuit,1000)