Snowflurry/en: Difference between revisions
No edit summary |
(Created page with "Quantum Circuit Object: qubit_count: 2 q[1]:──H────*── ¦ q[2]:───────X── }} </noinclude> In the above code section, the Hadamard gate creates an equal superposition of |0⟩ and |1⟩ on the first qubit while the CNOT gate (controlled X gate) creates an entanglement between the two qubits. We find an equal superposition of states |00⟩ and |11⟩, which is the first Bell state. The <code>simulate</code> function allows...") |
||
| Line 29: | Line 29: | ||
julia> print(circuit) | julia> print(circuit) | ||
Quantum Circuit Object: | Quantum Circuit Object: | ||
qubit_count: 2 | qubit_count: 2 | ||
| Line 37: | Line 36: | ||
}} | }} | ||
</noinclude> | </noinclude> | ||
In the above code section, the Hadamard gate creates an equal superposition of |0⟩ and |1⟩ on the first qubit while the CNOT gate (controlled X gate) creates an entanglement between the two qubits. We find an equal superposition of states |00⟩ and |11⟩, which is the first Bell state. The <code>simulate</code> function allows us to simulate the exact state of the system. | |||
<noinclude> | <noinclude> | ||
julia> state = simulate(circuit) | julia> state = simulate(circuit) | ||
| Line 47: | Line 46: | ||
0.7071067811865475 + 0.0im | 0.7071067811865475 + 0.0im | ||
</noinclude> | </noinclude> | ||
<div lang="fr" dir="ltr" class="mw-content-ltr"> | <div lang="fr" dir="ltr" class="mw-content-ltr"> | ||
Revision as of 20:29, 30 September 2024
Snowflurry
Developed in Julia by Anyon Systems, Snowflurry is an open-source quantum computing library to build, simulate and run quantum circuits. A related library called SnowflurryPlots shows simulation results in a bar graph. Useful to explore quantum computing, its features are described in the documentation and the installation guide is available on the GitHub page. Like the PennyLane library, Snowflurry can be used to run quantum circuits on the MonarQ quantum computer.
Installation
Le simulateur d'ordinateur quantique avec Snowflurry est accessible sur toutes nos grappes. Avant d'avoir accès à Snowflurry, il faur charger le langage de programmation Julia avec la commande
[name@server ~]$ module load julia
The Julia programming interface is then called and the Snowflurry quantum library is loaded (about 5-10 minutes) with the commands
[name@server ~]$ julia
julia> import Pkg
julia> Pkg.add(url="https://github.com/SnowflurrySDK/Snowflurry.jl", rev="main")
julia> Pkg.add(url="https://github.com/SnowflurrySDK/SnowflurryPlots.jl", rev="main")
julia> using Snowflurry
Quantum logic gates and commands are described in the Snowflurry documentation.
Use case: Bell states
Bell states are maximally entangled two-qubit states. They are simple examples of two quantum phenomena: superposition and entanglement. The Snowflurry library allows to construct the first Bell state as follows:
[name@server ~]$ julia
julia> using Snowflurry
julia> circuit=QuantumCircuit(qubit_count=2);
julia> push!(circuit,hadamard(1));
julia> push!(circuit,control_x(1,2));
julia> print(circuit)
Quantum Circuit Object:
qubit_count: 2
q[1]:──H────*──
¦
q[2]:───────X──
In the above code section, the Hadamard gate creates an equal superposition of |0⟩ and |1⟩ on the first qubit while the CNOT gate (controlled X gate) creates an entanglement between the two qubits. We find an equal superposition of states |00⟩ and |11⟩, which is the first Bell state. The simulate function allows us to simulate the exact state of the system.
julia> state = simulate(circuit)
julia> print(state)
4-element Ket{ComplexF64}:
0.7071067811865475 + 0.0im
0.0 + 0.0im
0.0 + 0.0im
0.7071067811865475 + 0.0im
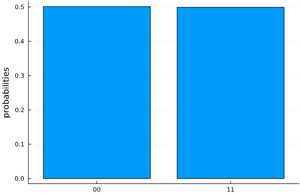
Pour effectuer une mesure, l'opération readout permet de spécifier quels qubits seront mesurés. La bibliothèque SnowflurryPlots et la fonction plot_histogram permettent de visualiser les résultats.
[name@server ~]$ julia
julia> using SnowflurryPlots
julia> push!(circuit, readout(1,1), readout(2,2))
julia> plot_histogram(circuit,1000)