Scalability/fr

[Note de la traduction : à défaut d’un meilleur terme, nous utilisons le calque scalabilité.]

En programmation parallèle, on définit la scalabilité comme étant la capacité que possède un programme à utiliser des ressources de calcul additionnelles, soit des cœurs CPU. Il serait naïf de croire que le fait de doubler le nombre de cœurs réduirait de moitié la durée d’une opération de calcul; c’est rarement le cas. Nous observons plutôt que le gain en performance dépend de la nature du problème, de l’algorithme ou du programme utilisé pour le résoudre, du matériel sous-jacent (notamment la mémoire et le réseau) ainsi que du nombre de cœurs CPU utilisés. Pour cette raison, quand vous prévoyez utiliser un programme parallèle sur une grappe en particulier, nous recommandons de faire d’abord une analyse de scalabilité en faisant varier le nombre de cœurs selon une certaine échelle (par exemple 2, 4, 8, 16, 32, 64 cœurs). Une telle analyse vous permettra de connaître le temps d’exécution dans chacun des cas et de voir la courbe des variations.

Deux raisons principales font que la scalabilité n’est pas toujours celle que nous souhaiterions ː

Premièrement, ce ne sont pas toutes les opérations qui peuvent être exécutées en parallèle et un certain pourcentage de l’exécution se fait en série. Ce pourcentage fixe un seuil à l’efficacité de la parallélisation. Par exemple, si la version série d’un programme prend une heure pour effectuer un calcul et que six minutes (10 % du temps) sont employées à des opérations qui ne sont pas parallélisables, il ne sera jamais possible d’atteindre une durée d’exécution de moins de six minutes, peu importe le nombre de cœurs qu'on ajoute. Tout ce qu’on peut espérer c’est que le pourcentage du temps effectué en série diminue au fur et à mesure que la taille du problème grandit.

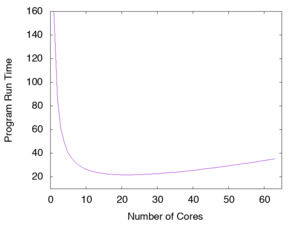
Deuxièmement, la parallélisation requiert habituellement une certaine part de communication et de synchronisation entre les processus qui travaillent en parallèle; cette charge additionnelle est en quelque sorte un coût indirect qui augmente de façon non linéaire avec le nombre de cœurs exprimé par $T_{c}\propto n^{\alpha }$ où $\alpha >1$. Supposons maintenant que le temps d’exécution de la partie scientifique du programme est employé également par chacun des cœurs (sans compter la partie résiduelle en série) et que $T_{s}=A+B/n$; le facteur déterminant de la durée totale d’exécution $T=T_{s}+T_{c}=A+B/n+Cn^{\alpha }$ (où $A$, $B$ et $C$ sont des nombres réels positifs dont les valeurs dépendent de la grappe, du programme et du problème) sera ici le coût indirect de la parallélisation quand $n\to \infty$. Si $A$ et $B$ sont beaucoup plus grands que $C$, le temps d’exécution par rapport au nombre de cœurs suivra la courbe représentée ici.

Remarquez que la durée d’exécution diminue lorsqu’on utilise peu de cœurs, puis qu’un minimum est atteint autour de $n\approx 22$ et enfin que la durée augmente avec l’ajout de processus, donnant foi au proverbe trop de cuisiniers gâtent la sauce. Quand vous utilisez un programme parallèle, il est primordial d’effectuer une analyse de scalabilité semblable afin d’identifier le nombre optimal de cœurs CPU entre 4, 128, 1024 ou autre, selon la nature et la taille du problème et selon la grappe sur laquelle le programme est exécuté.

Prenez soin de bien choisir le problème qui servira à cette analyse : il sera assez petit pour que les tests se fassent rapidement, tout en étant représentatif des cas réels que vous avez à traiter. Un problème nécessitant de 30 à 60 minutes avec un ou deux cœurs est probablement un bon choix alors qu’un test d’une durée de moins de 10 minutes serait d’une valeur douteuse. Dans certains contextes où on veut réduire la scalabilité (voir plus loin), le test devrait se faire avec un problème qui peut facilement être étendu, de façon relativement graduelle.

Dans le cas de problèmes où֫ l’élément $C$ (le problème lui-même) compte pour zéro, la charge additionnelle de parallélisation est inexistante; ces problèmes sont donc facilement parallélisables (embarrassingly parallel). Prenons l’exemple d’une analyse de 500 fichiers différents et indépendants les uns des autres où un seul nombre est généré et enregistré dans un vecteur. Dans un tel cas, les opérations des différents processus d’analyse n’ont pas besoin de synchronisation et les processus n’ont pas besoin de communiquer entre eux : la scalabilité du programme serait parfaite, peu importe le nombre de processus et l’unique limite serait imposée par le nombre de fichiers analysés.

Voyons maintenant deux formes de scalabilité. Si une meilleure scalabilité est habituellement souhaitable, il pourrait s’avérer préférable de l’atténuer dans certains cas, selon l’usage que vous voulez faire de plusieurs cœurs. Par exemple,

• si vous voulez effectuer plus rapidement les mêmes simulations, alors il est question de la scalabilité forte;
• si par contre vous voulez simuler des modèles plus grands ou plus détaillés sans augmenter la durée d’exécution, il s'agit de la scalabilité faible.

Scalabilité forte

Dans ce cas, le problème reste fixe alors que le nombre de cœurs augmente. On s’attendrait idéalement à une scalabilité linéaire, c’est-à-dire que la diminution du temps d’exécution par rapport à la valeur de référence serait réciproque au nombre de cœurs ajoutés. Dans l’exemple suivant, on peut constater le résultat de tests sur la même grappe d’un programme parallèle avec les paramètres d’entrée identiques :

nombre de cœurs	durée d’exécution (secondes)	efficacité (%)
2	2765	s.o.
4	1244	111,1
8	786	87,9
16	451	76,6
32	244	70,8
64	197	44,0
128	238	18,2

L’efficacité est le rapport de la durée d’exécution avec deux cœurs d’une part et $n$ cœurs d’autre part, divisé par $n/2$ puis multiplié par 100. La valeur du pourcentage indique le niveau de scalabilité linéaire de la performance parallèle, c’est-à-dire que le fait de doubler le nombre de cœurs réduit de moitié la durée d’exécution, ce qui correspondrait à une efficacité de 100 %.

Dans le tableau, passer de 2 à 4 cœurs résulte en une efficacité de plus de 100 %, ce qu’on appelle superlinear scaling. Il s’agit d’un cas qui est rare, mais qui se produit habituellement quand la cache fonctionne de plus en plus efficacement et que chacun des cœurs travaille de moins en moins.

Avec 128 cœurs, la durée d’exécution est plus grande qu’avec 64 cœurs (238 secondes contre 197) et l’efficacité est faible à 18 %.

Une efficacité de 75 % ou plus est à privilégier; dans cet exemple, nous recommanderions donc de soumettre les tâches sur 16 cœurs. Jusqu’à 64 cœurs, la durée d’exécution continue de décroître, mais l’amélioration obtenue avec plus de 16 cœurs serait une mauvaise utilisation des ressources.

Vous pouvez décider du nombre et de l’écart entre les points de contrôle. Nous recommandons d’utiliser au moins 5 ou 6 valeurs, mais si vous remarquez que le programme ralentit avec l’ajout de cœurs, il est évidemment inutile de poursuivre l’analyse au-delà de ce nombre.

Scalabilité faible

Pour diminuer la scalabilité, la taille du problème est augmentée en proportion de l’ajout de cœurs pour obtenir idéalement une scalabilité linéaire et que la durée d’exécution demeure stable. La taille du problème se caractérise différemment selon sa nature; il peut s’agir du nombre d’atomes pour une simulation moléculaire ou du nombre de cellules ou de nœuds du maillage pour une simulation en dynamique des fluides. Dans le tableau suivant, la taille du problème augmente proportionnellement à l’augmentation du nombre de cœurs.

nombre de cœurs	taille du problème	durée d’exécution (secondes)	efficacité (%)
1	1000	3076	-
4	4000	3078	99,9
12	12,000	3107	99,0
48	48,000	3287	93,6
128	128,000	3966	77,6

Le calcul de l’efficacité est simple : la durée d’exécution de référence (1 cœur) est divisée par la durée d’exécution avec $n$ cœurs et le résultat est converti en pourcentage. Encore une fois, l’objectif est d’atteindre une efficacité de 75 %. Comme c’est souvent le cas, l’efficacité demeure élevée avec plus de cœurs, contrairement à ce qui se produit avec l’augmentation de la scalabilité.

Une scalabilité moindre semble appropriée pour les programmes qui font un usage intensif de la mémoire. Elle est habituellement préférable quand un programme parallèle favorise la communication avec des entités à proximité, mais dans les cas contraires elle causera généralement une baisse de performance comme c’est le cas notamment avec la transformation de Fourier rapide.