Tutoriel OpenACC : Ajouter des directives
- comprendre le processus de transfert (offloading)
- comprendre ce qu'est une directive OpenACC
- connaitre la différence entre les directives loop et kernels
- savoir programmer avec OpenACC
- comprendre le concept d'alias en C/C++
- savoir utiliser la rétroaction du compilateur et éviter les faux alias
Transfert vers un processeur graphique (GPU)
Avant de porter du code sur un GPU, il faut savoir qu'ils ne partagent pas la même mémoire que le processeur (CPU); autrement dit, le GPU n'a pas un accès direct à la mémoire de départ. Cette dernière est en général plus grande, mais plus lente que la mémoire du GPU. Pour pouvoir utiliser un GPU, les données doivent passer par le bus PCI, dont la bande passante est moins grande que celles du CPU et du GPU. Il est donc de la plus haute importance de bien gérer les transferts entre la mémoire de départ et le GPU. En anglais, ce processus s'appelle offloading.
Directives OpenACC
Les directives OpenAcc sont semblables aux directives OpenMP. En C/C++, ce sont des pragmas et en Fortran, des commentaires. L'emploi de directives comporte plusieurs avantages. Premièrement, puisque le code est peu affecté, les modifications peuvent se faire de manière incrémentale, un pragma à la fois; ceci est particulièrement utile pour le débogage puisqu'il est ainsi facile d'identifier le changement précis qui crée le bogue. Deuxièmement, OpenACC peut être désactivé au moment de la compilation; les pragmas sont alors vus comme étant des commentaires et ne sont pas considérés par le compilateur, ce qui permet de compiler une version accélérée et une version normale à partir du même code source. Troisièmement, comme le compilateur fait tout le travail de transfert, le même code peut être compilé pour différents types d'accélérateurs, que ce soit un GPU, un Xeon Phi (MIC) ou un CPU; ainsi, un changement du matériel exigera simplement la mise à jour du compilateur, sans modification au code.
Le code de notre exemple contient deux boucles : la première initialise deux vecteurs et la seconde effectue une opération de niveau 1 d'addition des vecteurs.
| C/C++ | FORTRAN |
|---|---|
#pragma acc kernels
{
for (int i=0; i<N; i++)
{
x[i] = 1.0;
y[i] = 2.0;
}
for (int i=0; i<N; i++)
{
y[i] = a * x[i] + y[i];
}
}
|
!$acc kernels
do i=1,N
x(i) = 1.0
y(i) = 2.0
end do
y(:) = a*x(:) + y(:)
!$acc end kernels
|
Dans les deux cas, le compilateur identifie deux noyaux (kernels). En C/C++, les deux noyaux sont à l'intérieur de chaque boucle. En Fortran, les noyaux sont à l'intérieur de la première boucle et à l'intérieur de la boucle implicite effectuée lors d'une opération sur des tableaux.
Remarquez que le bloc OpenACC est délimité en C/C++ par des accolades; en Fortran, le commentaire est placé une fois au début et une dernière fois à la fin, avec l'ajout cette fois de end.
Boucles et kernels
Quand le compilateur lit la directive OpenACC kernels, il analyse le code pour identifier les sections pouvant être parallélisées. Ceci correspond souvent au corps d'une boucle. Dans ce cas, le compilateur délimite le début et la fin du corps du code avec la fonction kernel. Les appels à cette fonction ne seront pas affectés par les autres appels. La fonction est compilée et peut ensuite être exécutée sur un accélérateur. Comme chaque appel est indépendant, chacun des milliers de cœurs de l'accélérateur peut exécuter la fonction en parallèle pour un index spécifique.
| BOUCLE | KERNEL |
|---|---|
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
|
void loopBody(A,B,C,i)
{
C[i] = A[i] + B[i];
}
|
| Calcule de 0-N, dans l'ordre | Chaque cœur de calcul traite une valeur de i. |
La directive kernels
Cette directive est dite descriptive. Le programmeur l'utilise pour signifier au compilateur les portions qui selon lui peuvent être parallélisées. Le compilateur fait ce qu'il veut de cette information et adopte la stratégie qui lui semble la meilleure pour exécuter le code, incluant son exécution séquencielle. De façon générale, le compilateur
- analyse le code pour détecter le parallélisme,
- s'il détecte du parallélisme, identifie les données à transférer et décide quand faire le transfert,
- crée un kernel,
- transfère le kernel au GPU.
Voici un exemple de cette directive :
#pragma acc kernels
{
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
}
Il est rare que du code soit aussi simple et il faut se baser sur la rétroaction du compilateur pour trouver les portions qu'il a négligé de paralléliser.
Les utilisateurs d'OpenMP retrouveront dans OpenACC le principe de directives. Il existe cependant d'importantes différences entre les directives OpenMP et OpenACC. Les directives OpenMP sont à la base prescriptives. Ceci signifie que le compilateur est forcé d'accomplir la parallélisation, peu importe que l'effet détériore ou améliore la performance. Le résultat est prévisible pour tous les compilateurs. De plus, la parallélisation se fera de la même manière, peu importe le matériel utilisé pour exécuter le code. Par contre, le même code peut connaitre une moins bonne performance, dépendant de l'architecture. Il peut donc être préférable par exemple de changer l'ordre des boucles. Pour paralléliser du code avec OpenMP et obtenir une performance optimale dans différentes architectures, il faudrait avoir un ensemble différent de directives pour chaque architecture.
Pour leur part, plusieurs directives OpenACC sont de nature descriptive. Ici, le compilateur est libre de compiler le code de la façon qu'il juge la meilleure, selon l'architecture visée. Dans certains cas, le code ne sera pas parallélisé du tout. Le même code exécuté sur un GPU, sur un Xeon Phi ou sur un CPU peut donner du code binaire différent. Ceci signifie que la performance pourrait varier selon le compilateur et que les compilateurs d'une nouvelle génération seront plus efficaces, surtout en présence de nouveau matériel.
Exemple : porter un produit matrice-vecteur
Pour notre exemple, nous utilisons du code provenant du répertoire Github, particulièrement une portion de code du fichier matrix_functions.h. Le code Fortran équivalent se trouve dans la sousroutine matvec contenue dans le fichier matrix.F90. Le code original est comme suit :
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
Le premier changement à faire au code est d'ajouter la directive kernels pour essayer de le faire exécuter sur le GPU. Pour l'instant, nous n'avons pas à nous préoccuper du transfert des données ou à fournir des renseignements au compilateur.
#pragma acc kernels
{
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
}
Développer avec OpenACC
Dans ce tutoriel, nous travaillons avec la version 16.3 des compilateurs du Portland Group. Nous utilisons l'option -ta (pour target accelerator) pour porter le code sur les accélérateurs et la sous-option tesla:managed pour signifier au compilateur que les GPU Tesla sont la cible et que nous voulons utiliser une mémoire autogérée, ce qui simplifie le transfert de données dans les deux directions. Cette option ne sera pas utilisée dans un prochain exemple. Nous utilisons aussi l'option d'optimisation -fast. En résultat, nous constatons que le compilateur n'a pu paralléliser les deux boucles; nous verrons plus loin comment traiter ce cas.
[name@server ~]$ pgc++ -fast -Minfo=accel -ta=tesla:managed main.cpp -o challenge
...
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
27, Generating copyout(ycoefs[:num_rows])
Generating copyin(xcoefs[:],Acoefs[:],cols[:],row_offsets[:num_rows+1])
29, Complex loop carried dependence of row_offsets-> prevents parallelization
Loop carried dependence of ycoefs-> prevents parallelization
Loop carried backward dependence of ycoefs-> prevents vectorization
Complex loop carried dependence of cols->,Acoefs->,xcoefs-> prevents parallelization
Accelerator kernel generated
Generating Tesla code
33, #pragma acc loop vector(128) /* threadIdx.x */
37, Sum reduction generated for sum
33, Loop is parallelizable
As we can see in the compiler output, the compiler could not parallelize the two loops. We will see in the following sections how to deal with this.
En date de mai 2016, relativement peu de compilateurs offraient les fonctionnalités d'OpenACC. Les plus avancés en ce sens sont les compilateurs du Portland Group de NVidia et ceux de Cray. Pour ce qui de GNU, l'implémentation d'OpenACC était expérimentale et devrait être complète dans la version 6.
Dans ce tutoriel, nous utilisons la version 16.3 des compilateurs du Portland Group qui sont gratuits pour des fins de recherche universitaire.
Réparer les fausses dépendances de boucles
Même lorsque le programmeur sait qu'une boucle peut être parallélisée, il arrive que le compilateur ne le remarque pas. Un cas commun en C/C++ est connu sous le nom de 'pointer aliasing. Contrairement au Fortran, C/C++ ne possèdent pas comme tel de tableaux (arrays), mais plutôt des pointeurs. Le concept d'alias s'applique à deux pointeurs dirigés vers la même mémoire. Si le compilateur ne sait pas que des pointeurs ne sont pas des alias, il doit cependant le supposer. Dans l'exemple précédent, on voit clairement pourquoi le compilateur ne pouvait pas paralléliser la boucle. En supposant que les pointeurs sont identiques, il y a forcément dépendance des itérations de la boucle.
Mot-clé restrict
Une des manières de dire au compilateur que les pointeurs ne sont pas des alias est d'utiliser le mot-clé restrict, introduit à cette fin dans C99. Il n'y a toujours pas de manière standard pour ce faire en C++, mais chaque compilateur possède un mot-clé qui lui est propre. Dépendant du compilateur, on peut utiliser __restrict ou __restrict__. Les compilateurs du Portland Group utilisent __restrict. Pour savoir pourquoi il n'existe pas de standard en C++, consultez ce document. Ce concept est important pour OpenACC comme pour toute programmation C/C++, car les compilateurs peuvent effectuer plusieurs autres optimisations si les pointeurs ne sont pas des alias. Remarquez que le mot-clé se place après le pointeur puisque c'est à ce dernier qu'il se réfère, et non au type; autrement dit, la déclaration doit se lire float * __restrict A; plutôt que float __restrict * A;.
En déclarant un pointeur comme étant restraint, on s'assure qu'uniquement ce pointeur ou une valeur dérivée (comme ptr +1) pourra accéder à l'objet auquel il réfère, et ce pour la durée de vie du pointeur. Ceci est une garantie que le programmeur donne au compilateur; si le programmeur manque à son obligation, le comportement n'est pas défini. Pour plus d'information, consultez l'article Wikipédia restrict.
Boucle avec clause independent
Une autre façon de s'assurer que le compilateur traite les boucles de manière indépendante est de le spécifier explicitement avec la clause independent. Comme toute autre directive prescriptive, le compilateur y est obligé et l'analyse qu'il pourrait faire ne sera pas considérée. En reprenant l'exemple de la section La directive kernels, nous avons : :
#pragma acc kernels
{
#pragma acc loop independent
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
}
Produit matrice-vecteur
Revenons au cas du produit matrice-vecteur présenté plus haut. Notre recommandation pour éviter les faux alias est de définir les pointeurs comme étant restreints en remplaçant le code de matrix_functions.h.
double *Acoefs=A.coefs;
double *xcoefs=x.coefs;
double *ycoefs=y.coefs;
par le code
double *__restrict Acoefs=A.coefs;
double *__restrict xcoefs=x.coefs;
double *__restrict ycoefs=y.coefs;
We note that we do not need to declare the other pointers as restricted, since they are not reported as problematic by the compiler. With the above changes, recompiling gives the following compiler messages:
[name@server ~]$ pgc++ -fast -Minfo=accel -ta=tesla:managed main.cpp -o challenge
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
27, Generating copyout(ycoefs[:num_rows])
Generating copyin(xcoefs[:],Acoefs[:],cols[:],row_offsets[:num_rows+1])
29, Loop is parallelizable
Accelerator kernel generated
Generating Tesla code
29, #pragma acc loop gang, vector(128) /* blockIdx.x threadIdx.x */
33, Loop is parallelizable
How is ported code performing ?
Since we have completed a first step to porting the code to GPU, we need to analyze how the code is performing, and whether it gives the correct results. Running the original version of the code yields the following (performed on one of Guillimin's GPU node):
[name@server ~]$ ./cg.x
Rows: 8120601, nnz: 218535025
Iteration: 0, Tolerance: 4.0067e+08
Iteration: 10, Tolerance: 1.8772e+07
Iteration: 20, Tolerance: 6.4359e+05
Iteration: 30, Tolerance: 2.3202e+04
Iteration: 40, Tolerance: 8.3565e+02
Iteration: 50, Tolerance: 3.0039e+01
Iteration: 60, Tolerance: 1.0764e+00
Iteration: 70, Tolerance: 3.8360e-02
Iteration: 80, Tolerance: 1.3515e-03
Iteration: 90, Tolerance: 4.6209e-05
Total Iterations: 100 Total Time: 29.894881s
Running the OpenACC version yields the following:
[name@server ~]$ ./challenge
Rows: 8120601, nnz: 218535025
Iteration: 0, Tolerance: 4.0067e+08
Iteration: 10, Tolerance: 1.8772e+07
Iteration: 20, Tolerance: 6.4359e+05
Iteration: 30, Tolerance: 2.3202e+04
Iteration: 40, Tolerance: 8.3565e+02
Iteration: 50, Tolerance: 3.0039e+01
Iteration: 60, Tolerance: 1.0764e+00
Iteration: 70, Tolerance: 3.8360e-02
Iteration: 80, Tolerance: 1.3515e-03
Iteration: 90, Tolerance: 4.6209e-05
Total Iterations: 100 Total Time: 115.068931s
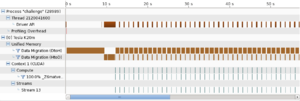
The results are correct. However, not only do we not get any speed up, but we rather get a slow down by a factor of almost 4! Let's profile the code again using NVidia's visual profiler (nvvp). This can be done with the following steps:
- Start nvvp with the command nvvp & (the & sign is to start it in the background)
- Go in File -> New Session
- In the "File:" field, search for the executable (named challenge in our example).
- Click "Next" until you can click "Finish".
This will run the program and generate a timeline of the execution. The resulting timeline is illustrated on the image on the right side. As we can see, almost all of the run time is being spent transferring data between the host and the device. This is very often the case when one ports a code from CPU to GPU. We will look at how to optimize this in the next part of the tutorial.
The parallel loop directive
With the kernels directive, we let the compiler do all of the analysis. This is the descriptive approach to porting a code. OpenACC supports a prescriptive approach through a different directive, called the parallel directive. This can be combined with the loop directive, to form the parallel loop directive. An example would be the following code:
#pragma acc parallel loop
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
Since parallel loop is a prescriptive directive, it forces the compiler to perform the loop in parallel. This means that the independent clause introduced above is implicit within a parallel region.
For reasons that we explain below, in order to use this directive in the matrix-vector product example, we need to introduce additional clauses used to manage the scope of data. The private and reduction clauses control how the data flows through a parallel region.
- With the private clause, a copy of the variable is made for each loop iteration, making the value of the variable independent from other iterations.
- With the reduction clause, the values of a variable in each iteration will be reduced to a single value. It supports addition (+), multiplication (*), maximum (max), minimum (min), among other operations.
These clauses were not required with the kernels directive, because the kernels directive handles this for you.
Going back to the matrix-vector multiplication example, the corresponding code with the parallel loop directive would look like this:
#pragma acc parallel loop
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
#pragma acc loop reduction(+:sum)
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
Compiling this code yields the following compiler feedback:
[name@server ~]$ pgc++ -fast -Minfo=accel -ta=tesla:managed main.cpp -o challenge
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
27, Accelerator kernel generated
Generating Tesla code
29, #pragma acc loop gang /* blockIdx.x */
34, #pragma acc loop vector(128) /* threadIdx.x */
Sum reduction generated for sum
27, Generating copyout(ycoefs[:num_rows])
Generating copyin(xcoefs[:],Acoefs[:],cols[:],row_offsets[:num_rows+1])
34, Loop is parallelizable
Parallel loop vs kernel
| PARALLEL LOOP | KERNEL |
|---|---|
|
|
Both approaches are equally valid and can perform equally well.
- Modify the functions matvec, waxpby and dot to use OpenACC. You may use either the kernels or the parallel loop directives. The directories step1.* contain the solution.
- Modify the Makefile to add -ta=tesla:managed and -Minfo=accel to your compiler flags.
Onward to the next unit: Data movement
Back to the lesson plan